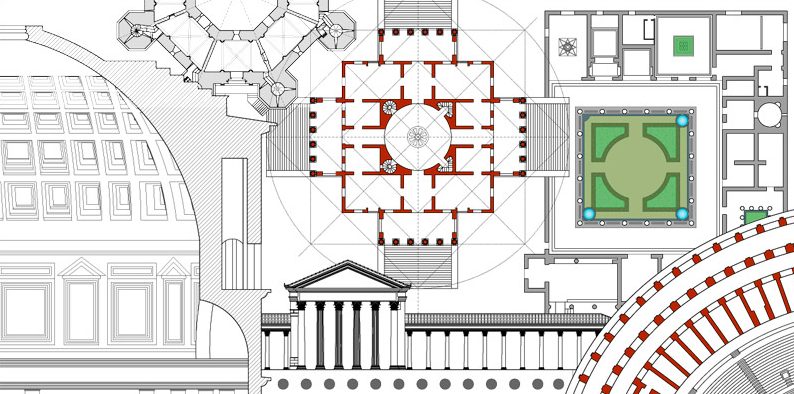
Golden Rectangle
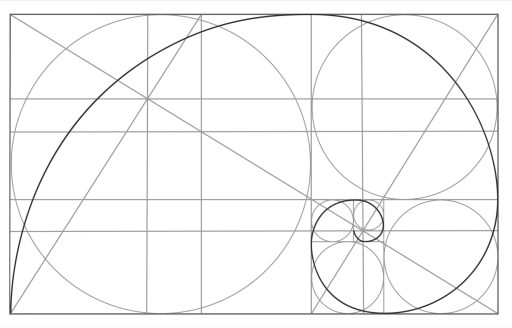
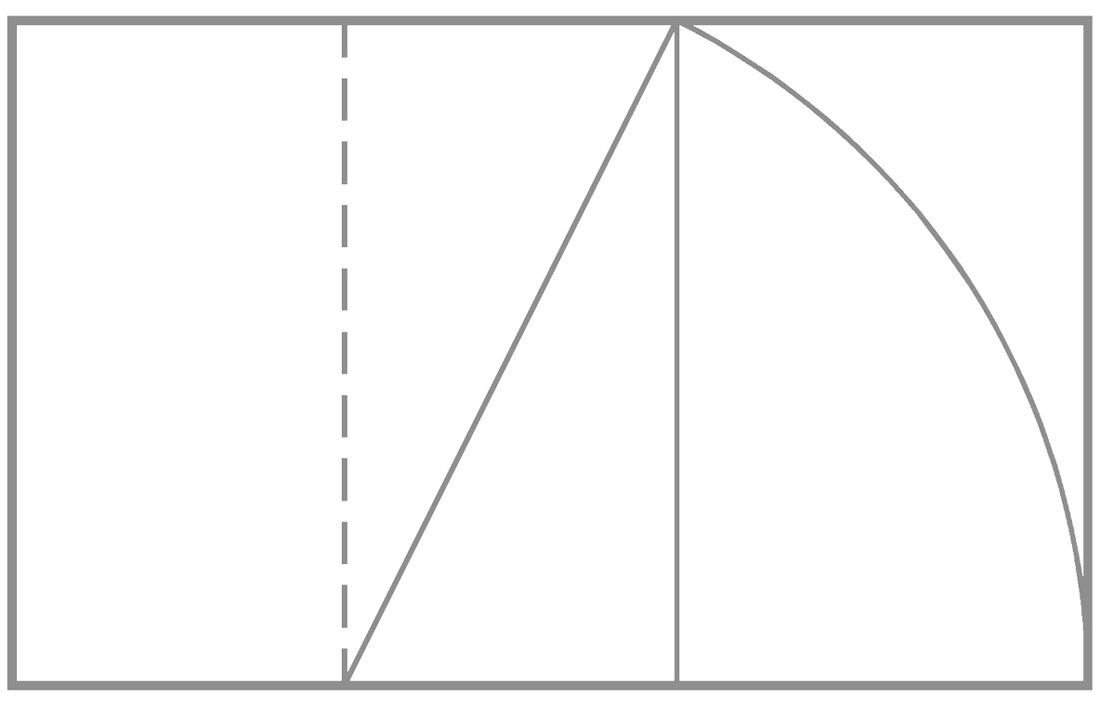
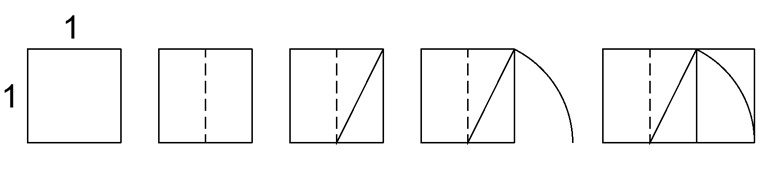
Construction of the golden rectangle
GOLD SECTION, GROWTH AND FIBONACCI SERIES
The golden rectangle, also known as the golden rectangle or golden ratio, is a special ratio between the lengths of the sides of a rectangle. A rectangle is said to be golden if the ratio of the length of the longer side to that of the shorter side is approximately equal to the ratio of the sum of the two lengths to the length of the longer side. Mathematically, this ratio is approximately equal to 1.6180339887… and is often represented by the Greek letter φ (phi). This ratio has been found to be aesthetically pleasing and has been used in many works of art and architecture.
Ø (fi), was described by Johannes Kepler as one of the “two great treasures of geometry” (the other was Pythagoras’ theorem).
The golden rectangle, with dimensions Ø and 1, can be easily constructed with a ruler and compass according to the technique shown in the image below. Click on the image to download the dwg.
From the golden rectangle, the golden spiral can be constructed.
Apparently, these ratios were known since Egyptian times, as they are found as particular harmonic ratios in the study of the dimensions of the pyramid of Cheops. Similar proportions are also found on the Parthenon in Athens.

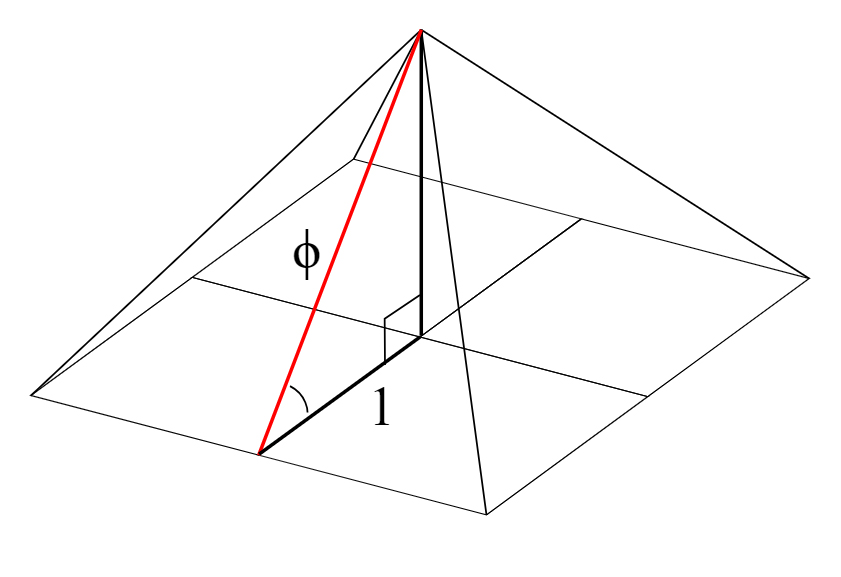

Wanting to construct a sequence of relationships in which the golden relationship between the new quantities is consistently preserved, one can proceed as follows:
(1-x):x=x:1=1:(1+x)=(1+x):(2+x)=(2+x):(3+2x)=(3+2x):(5+3x)=(5+3x):(8+5x)=
(8+5x):(13+8x)=(13+8x):(21+13x) ……
The numerical sequences we have thus obtained indicate precisely the close correlation with lo in the development of the Fibonacci sequence. This with increasing values comes closer and closer to a geometric progression of reason Ø.