Sezione aurea

Sezione aurea

Le sue proprietà geometriche e matematiche e la frequente riproposizione in svariati contesti naturali e culturali, apparentemente non collegati tra loro, hanno suscitato per secoli nella mente dell'uomo la conferma dell'esistenza di un rapporto tra macrocosmo e microcosmo, tra Dio e l'uomo, l'universo e la natura: un rapporto tra il tutto e la parte, tra la parte più grande e quella più piccola che si ripete all'infinito attraverso infinite suddivisioni.[1] Diversi filosofi e artisti sono arrivati a cogliervi col tempo un ideale di bellezza e armonia spingendosi a ricercarlo e, in alcuni casi, a ricrearlo nell'ambiente antropico quale canone di bellezza; testimonianza ne è la storia del nome che in epoche più recenti ha assunto gli appellativi di aureo e divino…..Wikipedia…>>

 A     M        B
 | 1-x |    x    |
 
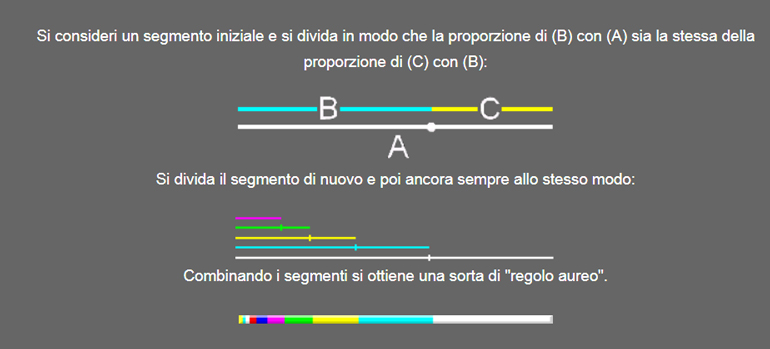
Il segmento AB viene diviso dal punto M in modo tale che il rapporto tra le due parti, la più piccola con la più grande (AM e MB), è uguale al rapporto della parte più grande (MB) con tutto AB.
 
Se AB è di lunghezza 1, e chiamiamo x la lunghezza del segmento MB, allora la definizione sopra fornita dà luogo alla seguente equazione:
 
     1 – x    =   x   , e cioè   1-x = x²
       x            1

che ha due soluzioni per x, (-1-√5)/2 and (√ 5-1) / 2. 

La prima è negativa, per cui non soddisfa le condizioni del problema. La seconda rappresenta proprio il rapporto di sezione aurea ed è un numero irrazionale corrispondente a circa 0,618. 
Il reciproco di x (1/x) viene indicato con Ø e corrisponde a 1+x, cioè circa 1,618. Molto spesso questo rapporto viene indicato come rapporto aureo e viene utilizzato nella costruzione del rettangolo aureo.
La costruzione della sezione aure suggerisce la possibilità di realizzare un processo di crescita in cui si conservano costantemente i rapporti, cioè la crescita dà luogo ad  organismi che rimangono sempre simili a se stessi.